Unit VIII. Kinetics, Equilibria & Thermodynamics. Ch. 5, 14, 15, & 19

I. Chemical Reactions & Thermodynamics:  A reaction is a process where matter undergoes a change in composition. This change 

in composition is commonly associated with a change in the energy states of the materials.

    A. Energy- A characteristic of an object as defined it's ability to do work or transfer heat.

        1. Potential Energy is the energy associated with the position or location of an object relative to another.  

            Ex. book on a desk or electrons in energy levels.

        2. Work is defined by moving an object in the direction of an applied force.  Work in chemistry would be the energy needed 

            to overcome attractive forces (inter- & intramolecular forces). 

            Ex. lifting a book against gravity or moving electrons against nuclear force (Z_eff)

        3. A Chemical reaction then represents a change in potential energy:

                Energy_(Reactants) à Energy_{(Transition State)} à Energy_(Products)

    B. Kinetic Molecular Theory- Molecules require a certain amount of energy and correct orientation in order to react.

1.       Activation Energy (E_a)- The minimum amount of energy that reactants require in order to react. This represents the 

        transition state of a reaction.

      Svante Arrhenius proposed this concept based on the kinetic energy of the particles.  The Maxwell-Boltzman distribution

      curve potentially identifies the particles (with highest K.E.) that can obtain this activation energy.  The energy needed to 

      overcome inter- & intramolecular attractions.

Energy Profile for a chemical reaction

    C. Free Energy- The energy difference between reactants and products

        1. First Law of Thermodynamics- (Law of Conservation of Energy).  Energy can neither be created nor destroyed, but can change forms.

        The total energy (system & surroundings) must be conserved.

        2. Enthalpy Changes (DH): The heat changes associated with chemical & physical changes. Results from changes in potential energy of the     

                reactants and products.

   calorie- a unit of heat energy.  The energy needed to raise 1 g of water by 1 C^o. 

           4.184 J = 1 cal

    a. Enthalpies of Reaction- The change in heat energy associated with a chemical reaction. 

         i.  Exothermic (-DH)- Energy is released (system à surroundings); PE_(reactants) >  PE_(products)

                Exothermic reaction tend to be spontaneous because they reduce the energy of a system.

                Exothermic processes are typically irreversible.

        ii. Endothermic (+DH)- Heat is absorbed (surroundings à system); PE_(reactants) <  PE_(products)

        iii. Thermochemical equations:  Chemical equations that also include the enthalphy change

            Ex.     2H₂(g)  +  O₂(g)  --> 2H₂O(g)  + 483.6 kJ

                This is exothermic because energy is a product so DH = -483.6 kJ.

        iv. Characteristics

            1. Enthalpy changes are dependent upon the mass of the reactants (extensive property)

            2. Enthalpy changes are numerically equivalent but opposite in sign for the reverse reactions

            3. Enthalpy changes are dependent upon the state of the reactants and products.

    b. Hess's Law- Chemical reactions can be considered to exist in individual steps and the total enthalpy change is the sum of the enthalpies for each step.

Practice:  Hess's Law

    c. Enthalpies of Formation (DH_f)- The enthalpy change associated with the production of 1 mol of a compound from its constituent elements in their standard state.

        i. Standard enthalpy of formation (DH_f^o)- The enthalpy of formation at Standard State (1atm & 25 ^oC)

            The DH_f^o for any element in its most stable form is zero.

         ii. For any reaction, the enthalpy of reaction is the stoichiometric sum of the individual enthalpies of formation

                    where DH₁ = n₁(DH_f^o) ;  n₁ is the stoichiometric equivalence for compound 1.

                               Re: DH_f^o for a reactant is a negative value because we are not forming it, but breaking it down.

                    iii. Born-Haber Cycle- An indirect process for calculating the lattice energy of an ionic salt by using Hess's Law, enthalpy of formations and energy diagrams.

                        -lattice energy is a measure of strength of attraction of ions in an ionic salt. The attraction of ions is an exothermic process which will yield a -DH value.

Practice:  Born-Haber Cycle

    3. Entropy: The measure of disorder associated with a system. Entropic changes are temperature dependent (TDS)

a. Entropy Changes (DS): State functions that describe the energy changes associated with a change in order. 

     where q is the energy that is transferred into the system during a spontaneous, reversible process.

            i. Enthalpy changes changes with phase changes (DH_vap & DH_fus)

            ii. Enthalpy changes associated with chemical changes (DH_f^o)

    Entropy changes also occur during isothermal expansions/contractions of gases

Changes that increase entropy (+DS) tend to be spontaneous.

b. 2^nd Law of Thermodynamics- For a spontaneous change in the universe to take place at constant temperature and pressure, 

    the entropy of the universe must increase. 

        -This applies to any closed system where DH is zero.

            c. The entropy of a pure crystalline element or compounds at absolute zero is zero. 

                -At absolute zero, an object has zero kinetic energy.  This means there is no motion and therefore no stored energy. 

                The degrees of freedom for the particles is zero.

            d. Entropy changes occur when:

                i. Liquids or solutions a formed from solids

                ii. Gases are formed from either solids or liquids

                iii. The moles of gas molecules increases during a chemical reaction

                iv. The temperature of a substance increases

Diagram: Comparing phase changes and entropy.

    4. Free Energy:  The total energy change associated with a system. (Enthalpy & Entropy)

        Gibbs-Helmholtz Free Energy: 

a. Endergonic:  (+DG): The total energy is increased in the system. 

b. Exergonic: (-DG): The total is decreased from  the system. 

c. Spontaneous processes requires a release of free energy

    i. If DG is negative, the reaction is spontaneous in the forward direction

    ii. If DG is zero, the reaction is at equilibrium

    iii. If DG is positive, the reaction requires an input of energy from the surroundings in order for the reaction to proceed.

        The reverse reaction will be spontaneous.

II. Kinetics- The study of the rates of chemical reactions. 

     Factors that determine the rates of reactions:

1.   Concentration of reactants

2.      Temperature of the reaction

3.      Presence of a catalyst

4.      Surface area of the reactants or catalyst.

    A. Collision Theory:  Reactions require that reactants interact with each other (or with itself for decomposition) with ample kinetic 

        energy into order to constrain the bonds that hold these particles together. 

        These previous four factors are simple ways in which particles interact at a greater rate

1.Activation Energy:  Svante Arrhensius proposed that molecules require a specific amount of kinetic energy in order to react. 

    -The number of particles possessing this kinetic energy can be identified on a Maxwell-Boltzman distribution graph.

    B. Reaction Rates- The concentration change of a reactant or product as a function of time. 

            1. Average reaction rate = Change in the number of moles of a substance/ change in time. 

                 Reaction rates are typically measured in concentration changes per time.   (M/s)

                                For the General Reaction:   rR --> pP

                a. average rate of appearance. The rate at which a product is produced

                b. average rate of disappearance. The rate at which a reactant is consumed

Question: As a reaction proceeds, the rate is not constant.  WHY?

           2. Instantaneous reaction rate = The rate at any one time. Tangent to the curve at one point along a concentration curve.

Questions:  Does concentration effect the rate of collisions?  If so, what happens to the rate as a function of concentration changes?

     C. Rate Laws:  Reaction rates are dependent upon the concentration of reactants.

                    Rate a [reactants] ;   so Rate = k [reactants] where k is the rate law constant.

        1. Reaction Order-  Describes the stoichiometric relationship for any rate law.

                For any reaction:                 

             a. the reaction orders are found experimentally and do not necessarily match the coefficients of the balanced equation.

                -to calculate the reaction order, determine what factor of rate change occurs as a function of concentration changes.

            b. The overall reaction order is the sum of the individual reaction orders.

            c. the units of k are dependent upon the individual reaction orders.                      

                 Once k and the reaction orders are found, the rate for any concentration can be calculated.

            d. the concentrations of products (for reversible reactions) is not considered because rate law expressions are written

                when the reverse reaction is insignificant, usually at t = 0. 

        2. First-Order Reactions. The rate of a reaction is dependent upon the concentration of 1 reactant raised to the first power.

            a. To solve for the concentration of a reactant at any time, knowing:

                1. initial concentration

                2. rate law constant

                3. first order reaction

                    The graph of ln[A] vs time is a linear graph.  

Review: Natural Log Functions.

            b. Half-Life- The time required for the concentration of a reactant to decrease to 1/2 of the original concentration.

                At the Half-Life,  [A]_t = 1/2 [A]₀

                1. For a first order reaction, the half life is equal to:

        4. Second-Order Reactions: A reaction where the rate depends upon the square of the reactant's concentration.

            a. To solve for the concentration of a reactant at any time, knowing:

                1. initial concentration

                2. rate law constant

                3. second order reaction   

            b. Half-Life for a second order reaction:

    D. Temperature and Rates.

        -Arrhenius calculated that reaction rates do not express a linear relationship with temperature.  This is explained by

        Maxwell-Boltzmann distribution. As the temperature of the particles increase, the number of particles containing

        "critical Kinetic energy" increases in a non-linear fashion.

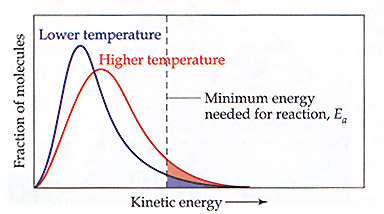
           Chemistry. The Central Science. Brown, LeMay & Bursten

            This relationship shows that the rate increases must be a function of rate law constant changes and not changes

            in concentration (from Rate = k[A]).  Arrehenius also established a relationship that activation energy changes can also

            affect rates, thus changing the rate law constant.

            Simplifying Arrhenius' Equation for changes in k as a function of changes in T is accomplished by the following

Question:  Why don't stoichiometric relationships establish the reaction orders? 

     E. Elementary Steps

            Reactions typically proceed as series of multi-step elementary reactions. The overall reaction is dependent upon the rates

           of these individual reactions.  

        1. Molecularity- The stoichiometric relationship between the reactants in an elementary step. 

            a. unimolecular- One molecule is involved in the step

            b. bimolecular- Two molecules are involved in the step

            c. termolecular- Three molecules are invovled in the step.

                * As the number of molecules increases in a step, the probability that correct collisions occur, decreases significantly.

        2. Intermediate- An unstable product from one elementary step that gets used as a reactant in another.  These are not part

            of the overall chemical reaction.

        3. Rate and Elementary steps.

            a. Rate limiting step.  The elementary step that proceeds slower than the rest and therefore dictates the overall reaction

                rate.  The molecularity of the rate limiting step will typically determine the rate law.

            b. Non-rate limiting step.  The step(s) that is(are) faster and therefore don't necessarily affect the overall reaction rate.

                Example:  NO_2(g)  +  CO_(g) ->  NO_(g) + CO_2(g)

            c. Rate Laws that include an intermediate. This typically occurs when the first step is fast and a following step is slow.

                1. A fast first step creates an intermediate that is allowed to build up because a following step is slow.  Intermediates

                   are unstable which means the fate of an intermediate has 2 paths, react to form the products or decompose back into

                    the original reactants.

                    Ex.  2NO_(g)  +  O_2(g)  -> 2NO_2(g)

                        The observed rate law is:    Rate = k[NO]²[O₂]

                              The generally accepted mechanism for this is:

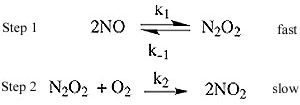
                            If we determined that the rate law is based on the molecularity of slow elementary step then the rate law would

                            look like this:

            Rate = k₂ [N₂O₂] [O₂]       (1a.)

                            But we don't want a rate law that involves an intermediate.  These are unstable and therefore concentrations are

                            very difficult to assess.  But N₂O₂ is involved in an equilibrium expression with NO, so:

Rate_(forward) =  Rate_(reverse)

k₁[NO]²    =    k_-1[N₂O₂]

                            by solving for [N₂O₂]                                   [N₂O₂] = k₁/k_-1 [NO]²

                            substitute back into the rate law (1a.)      Rate = k₁k₂/k_-1 [NO]² [O₂]

                            k₁k₂/k_-1 is equal to k overall so:              Rate = k [NO]² [O₂]

III. Chemical Equilbria

    A. Chemical Equilibrium. The condition where the rates of opposing reactions are equal.  The changes in concentrations of

        reactants and products are zero.

        1. A process at equilibrium must consist of opposing processes.  As a reaction () begins, the concentration

            of A ([A]) is high and the concentration of B ([B]) is zero.  The rate of disappearance of A is high because A would

            have most particles containing the "critical Kinetic Energy".  As the reaction progresses, the concentration of B increases

            which increases the number of B particles that will possess their own "critical KE" for the reverse reaction. 

        2. The concentrations of the reactants and products at equilibrium are not necessarily equal, even though their rates of

            production are equal.  Their concentrations are dependent more on the thermodynamics associated with each process. 

            The forward reaction may be more favored if DG_f < DG_r, or activation energy becomes very large for the reverse reaction. 

            The more negative DG of the forward reaction is the larger the activation energy of the reverse reaction. This would be

            seen as favoring the production of the products and not reactants, so equilibrium tends to the right.

            a. Equilibrium Expression. A mathematical expression that relates the concentrations of reactants and products as a

                function of the equilibrium.  This was first proposed by Guldber and Waage according to their Law of Mass Action.

                    For the reaction:                 

                    The K_eq for the reverse reaction is the reciprocal for the forward reaction.  Keep in mind that equilibrium is

                    independent direction in which it was achieved. What is important through is making sure that each K_eq is written

                    to express the concentration of their specific products to reactants.

                    The concentration of a solid or a pure liquid is typically constant throughout a reaction.  This will be omitted from

                    equilibrium expressions.

            b. If the substances are gases, pressure is proportional to the number of moles of particles as is concentration for

                solutions. In an equilibrium expression, for gases, we can merely use gas pressures as the ratio of particles at

                equilibrium.               

               The equilibrium constant can tell us which substances are favored, reactants or products.

                1. If K_eq >> 1 then the products are favored and equilibrium lies to the right

                2. If K_eq << 1 then the reactants are favored and the equilibrium lies to the left.

            c. Solving for equilibrium constants or equilibrium concentrations.

                To solve for a Keq constant, the concentrations of each component needs to be known. It is easily approached by

                setting up a table in order to express concentrations and change in concentrations.

                For a reaction that attains equilibrium, you will have to approach it by finding the changes in concentrations ( D [ ] )

                from the concentrations at time zero ( [ ]_to ).  The difference will give you the concentrations at equilibrium ( [ ]_te)