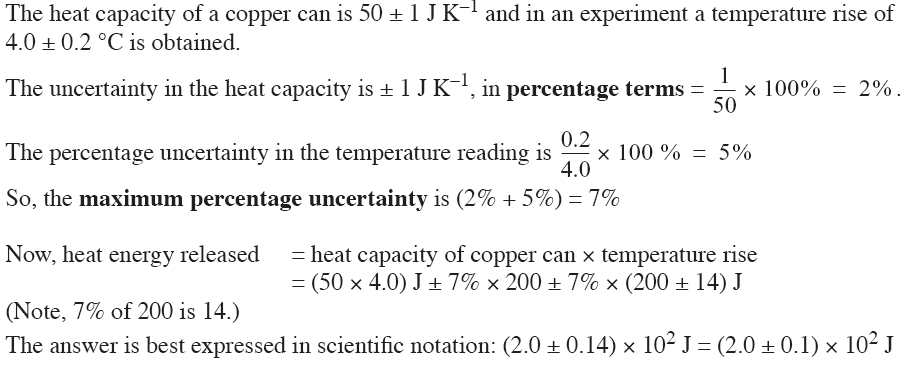USING SIGNIFICANT FIGURES
The number of
significant figures in a numerical result is an indication of the accepted error ina number. In counting the number of significant figures the problem is the digit zero (0). There
are five rules used in counting the number of significant figures in a number:
1. All non-zero digits are significant
,e.g., 12.3 has three significant figures and 549 has three significant figures.
2. Zeros between non-zero digits are significant
,e.g, 1.03 has three significant figures and 4023 has four significant figures.
3. Zeros at the end of a number are significant
,For numbers with decimal points, zeros to the right of a non zero digit are significant. E.g.,
2.00 has three significant figures, but 0.050 has two (the 5 & 0 in the second and third
decimal places).
4. Zeros to the left of the first non zero digit are not significant,
e.g., 0.84 has two significant figures: eight and four. The zero is termed a
placeholder
, meaning the zero is not part of the measurement, i.e., it is not significant.
5. Zeros at the end of a number without a decimal point are ambiguous,
e.g., 80 may have two significant figures or it may have one – the eight – with the zero
being a place holder. Only the person who carried out the measurement would know.
The ambiguity can be removed by reporting such numbers in
scientific or standard notation. Writing 80 as 8 x 101means that only one significant figure is present, while writing it as 8.0 x 101 means that two significant
figures are present.
6. Many physical constants, have a very large
number of digits,e.g., the speed of light in a vacuum,
c (299 792 458 m s–1).
7. Mathematical constants,
e.g., a number such as pi (
p) has an infinite number of digits
8. Logarithms can only retain in their mantissa the same number of significant figures
as there are in the number whose logarithm you are taking.
Note: your calculator will give as many figures as it has room to display, but they are not all significant. Another
problem with calculators is that they usually omit trailing zeros (see above) to the right of the decimal place,
which, as indicated in 3, are significant. Never copy numbers from your calculator without thinking about them
and repeating the calculation!
In theory, infinite, but in practice limited by the precision of the measuring device.
§ 9: SIGNIFICANIGURES
ROUNDING OFF
Sometimes it is necessary
to round off, to give the correct number of significant figures.
1.
A digit of 5 or larger rounds up.2.
A digit smaller than 5 rounds down.For example, rounding 13.654 to three significant figures gives 13.7 (the 4 is ignored, the 5 rounds up).
For example, rounding 13.246 to three significant figures gives 13.2 (the 6 is ignored, the 4 rounds down).
(Significant figures are discussed on pages 45 – 47 of
Chemistry for use with the InternationalBaccalaureate
2nd edition by John Green and Sadru Damji).EXAMPLE
In an experiment to measure the enthalpy change of reaction the following measurements were made:
mass of water = 58.000 ± 0.0005 g
temperature change of water = 12.5 ± 0.05
°CHeat released = mass of water
× specific heat capacity of water × change in temperature
= 58.000 g
× 4.184 J g –1 °C–1 × 12.5 °C = 3033.4 J
The temperature change was the
least precise measurement (three significant figures) so the result cannot be expressed as having more than three significant figures. Therefore the answer is 3030 J or, better still, 3.03 × 103 J and not 3033.4 J.
It is unacceptable to report values with more significant figures than indicated by the associated
uncertainty. For example, in 8.37 ± 0.2 cm the seven has no meaning and the length should be
reported as 8.3 ± 0.2 cm.
Higher Level Students Only
TREATMENT OF UNCERTAINTIES IN CALCULATIONS
During an experiment there will be a number of uncertainties which will have to be considered to give the overall uncertainty. This is known as the
propagation of uncertainties.
ADDING OR SUBTRACTING MEASURED QUANTITIES WITH ASSOCIATED UNCERTAINTIES
The maximum absolute uncertainty is the sum of the individual uncertainties.
1.
Dealing with uncertainties when one value is being subtracted from another
EXAMPLE
If the values of two temperatures are 36.3 ± 0.1
°C and 56.3 ± 0.1°C, find the difference.We first subtract the nominal values (56.3 – 36.3) = 20.0 °C.
Then, the absolute uncertainties are 0.1 and 0.1, so we add these, (0.1 + 0.1) = 0.2.
The final answer is 20.0 ± 0.2
°C.
2.
Dealing with uncertainties when one value is being added to another
EXAMPLE
If the values of two temperatures are 36.3 ± 0.1
°C and 56.3 ± 0.3°C, find the sum.We first add the nominal values (56.3 + 36.3) = 92.6 °C.
The absolute uncertainties are 0.3 and 0.1, so we add these, 0.3 + 0.1 = 0.4.
The final answer is 92.6 ± 0.4
°C.
The rule for both examples above is to add absolute uncertainties.
MULTIPLYING OR DIVIDING MEASURED QUANTITIESWITH ASSOCIATED UNCERTAINTIES
If uncertainties are to be multiplied or divided then percentage uncertainties have to be used (to take into account that the physical quantities will have different units).
The maximum percentage uncertainty is the sum of the percentage uncertainties for eachof the individual quantities.
-The rules applied here simplify the computation, but slightly exaggerate the uncertainty at each step. Note that formal mathematical notation is not used.
§ 10: PROPAGATION OF
EXAMPLE
If we want to calculate the power developed during an energy change of 44.01 ± 0.05 J, and the time over which it occurred, namely 2.10 ± 0.05 s, we
1.
take each of the uncertainties,2.
divide it by the given value, and then,3.
multiply by 100 to obtain a percentage.

Note that the relative uncertainty must be converted back into an absolute uncertainty:
i.e., 21 J s
–1 ± 2.5% = ± 0.52, but to one significant digit i.e. ± 0.5 since uncertainties are themselves approximate and are not given to more than one significant figure. Therefore.The rule is to convert the absolute uncertainties to percentage uncertainties, then convert them
back to an absolute uncertainty after the calculation.
EXAMPLE (THERMOCHEMISTRY)