Unit VIII. Kinetics

Kinetics- The study of the rates of chemical reactions. 

     Factors that determine the rates of reactions:

1.   Concentration of reactants

2.      Temperature of the reaction

3.      Presence of a catalyst

4.      Surface area of the reactants or catalyst.

    A. Collision Theory:  Reactions require that reactants interact with each other (or with itself for decomposition) with ample kinetic 

        energy into order to constrain the bonds that hold these particles together. 

        These previous four factors are simple ways in which particles interact at a greater rate

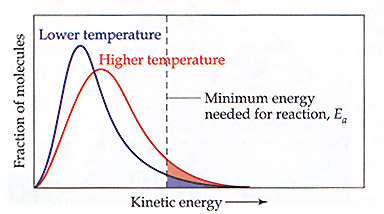
1.Activation Energy:  Svante Arrhensius proposed that molecules require a specific amount of kinetic energy in order to react. 

    -The number of particles possessing this kinetic energy can be identified on a Maxwell-Boltzman distribution graph.

    B. Reaction Rates- The concentration change of a reactant or product as a function of time. 

            1. Average reaction rate = Change in the number of moles of a substance/ change in time. 

                 Reaction rates are typically measured in concentration changes per time.   (M/s)

                                For the General Reaction:   rR --> pP

                a. average rate of appearance. The rate at which a product is produced

                b. average rate of disappearance. The rate at which a reactant is consumed

Question: As a reaction proceeds, the rate is not constant.  WHY?

           2. Instantaneous reaction rate = The rate at any one time. Tangent to the curve at one point along a concentration curve.

Questions:  Does concentration effect the rate of collisions?  If so, what happens to the rate as a function of concentration changes?

     C. Rate Laws:  Reaction rates are dependent upon the concentration of reactants.

                    Rate a [reactants] ;   so Rate = k [reactants] where k is the rate law constant.

        1. Reaction Order-  Describes the stoichiometric relationship for any rate law.

                For any reaction:                 

             a. the reaction orders are found experimentally and do not necessarily match the coefficients of the balanced equation.

                -to calculate the reaction order, determine what factor of rate change occurs as a function of concentration changes.

            b. The overall reaction order is the sum of the individual reaction orders.

            c. the units of k are dependent upon the individual reaction orders.                      

                 Once k and the reaction orders are found, the rate for any concentration can be calculated.

            d. the concentrations of products (for reversible reactions) is not considered because rate law expressions are written

                when the reverse reaction is insignificant, usually at t = 0. 

        2. First-Order Reactions. The rate of a reaction is dependent upon the concentration of 1 reactant raised to the first power.

            a. To solve for the concentration of a reactant at any time, knowing:

                1. initial concentration

                2. rate law constant

                3. first order reaction

                    The graph of ln[A] vs time is a linear graph.  

Review: Natural Log Functions.

            b. Half-Life- The time required for the concentration of a reactant to decrease to 1/2 of the original concentration.

                At the Half-Life,  [A]_t = 1/2 [A]₀

                1. For a first order reaction, the half life is equal to:

        4. Second-Order Reactions: A reaction where the rate depends upon the square of the reactant's concentration.

            a. To solve for the concentration of a reactant at any time, knowing:

                1. initial concentration

                2. rate law constant

                3. second order reaction   

            b. Half-Life for a second order reaction:

    D. Temperature and Rates.

        -Arrhenius calculated that reaction rates do not express a linear relationship with temperature.  This is explained by

        Maxwell-Boltzmann distribution. As the temperature of the particles increase, the number of particles containing

        "critical Kinetic energy" increases in a non-linear fashion.

           Chemistry. The Central Science. Brown, LeMay & Bursten

            This relationship shows that the rate increases must be a function of rate law constant changes and not changes

            in concentration (from Rate = k[A]).  Arrehenius also established a relationship that activation energy changes can also

            affect rates, thus changing the rate law constant.

            Simplifying Arrhenius' Equation for changes in k as a function of changes in T is accomplished by the following

Question:  Why don't stoichiometric relationships establish the reaction orders? 

     E. Elementary Steps

            Reactions typically proceed as series of multi-step elementary reactions. The overall reaction is dependent upon the rates

           of these individual reactions.  

        1. Molecularity- The stoichiometric relationship between the reactants in an elementary step. 

            a. unimolecular- One molecule is involved in the step

            b. bimolecular- Two molecules are involved in the step

            c. termolecular- Three molecules are invovled in the step.

                * As the number of molecules increases in a step, the probability that correct collisions occur, decreases significantly.

        2. Intermediate- An unstable product from one elementary step that gets used as a reactant in another.  These are not part

            of the overall chemical reaction.

        3. Rate and Elementary steps.

            a. Rate limiting step.  The elementary step that proceeds slower than the rest and therefore dictates the overall reaction

                rate.  The molecularity of the rate limiting step will typically determine the rate law.

            b. Non-rate limiting step.  The step(s) that is(are) faster and therefore don't necessarily affect the overall reaction rate.

                Example:  NO_2(g)  +  CO_(g) ->  NO_(g) + CO_2(g)

            c. Rate Laws that include an intermediate. This typically occurs when the first step is fast and a following step is slow.

                1. A fast first step creates an intermediate that is allowed to build up because a following step is slow.  Intermediates

                   are unstable which means the fate of an intermediate has 2 paths, react to form the products or decompose back into

                    the original reactants.

                    Ex.  2NO_(g)  +  O_2(g)  -> 2NO_2(g)

                        The observed rate law is:    Rate = k[NO]²[O₂]

                              The generally accepted mechanism for this is:

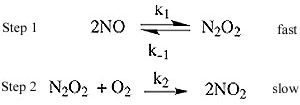
                            If we determined that the rate law is based on the molecularity of slow elementary step then the rate law would

                            look like this:

            Rate = k₂ [N₂O₂] [O₂]       (1a.)

                            But we don't want a rate law that involves an intermediate.  These are unstable and therefore concentrations are

                            very difficult to assess.  But N₂O₂ is involved in an equilibrium expression with NO, so:

Rate_(forward) =  Rate_(reverse)

k₁[NO]²    =    k_-1[N₂O₂]

                            by solving for [N₂O₂]                                   [N₂O₂] = k₁/k_-1 [NO]²

                            substitute back into the rate law (1a.)      Rate = k₁k₂/k_-1 [NO]² [O₂]

                            k₁k₂/k_-1 is equal to k overall so:              Rate = k [NO]² [O₂]