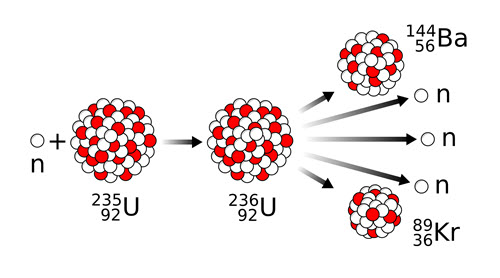
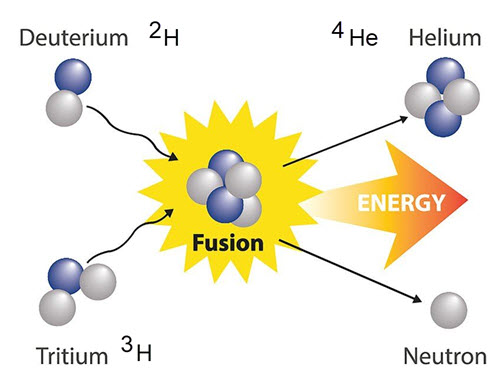
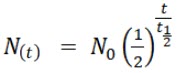Unit II.  Nuclear Chemistry

 

I. Introduction to Nuclear Reactions.

A. Chemical Reactions

Matter undergoes a change in composition where atoms are rearranged.

Law of Conservation of Matter:  The type and number of atoms are conserved in a normal chemical reaction

If the matter is conserved, then mass is conserved.

 Mass of Reactants = Mass of Products

B. Nuclear reactions.

Matter undergoes a transformation where new matter is made. Atoms are not necessarily conserved.

Mass is then not necessarily conserved.

 

II. Radioactivity

 

A. Nucleons-  The components of the nucleus.  Protons (11p) and Neutrons (10n)

1. atomic number (Z)- the number of protons

2. mass number (A)- the number of nucleons in an atom (protons + neutrons)

3. isotopes- atoms of the same elements that differ by the number of neutrons

a. nuclide- the nucleus of specific isotope of a certain element

4. radioisotope- an isotope that contains an unstable nuclide.

a. radionuclide- the unstable nucleus of a radioisotope

 

Video:  Radioactivity-Expect the Unexpected

Resource: The story of how radioactivity was discovered -- timeline

Resource: The theory behind radioactivity and nuclear stability

B. Atom construction & energies

Question:  What comprises the helium atom?

2 protons (@ 1.0073 a.m.u), 2 neutrons (@1.0087 a.m.u.) and 2 electrons (@ 0.00055 a.m.u)

Therefore the pieces of the helium atom add up to 4.0331 a.m.u.-- Isotopes of Helium

Helium-4 (99.999% of all helium atoms) has a mass of 4.0026.  Where does the other 0.0305 a.m.u. go?

 

1. Mass Defect- the difference in masses between the atom and the sum of the atom's components.

2. Nuclear Binding Energy- the energy associated with the mass defect defined by Einstein's equation  (E = mc2). It is the energy associated with nucleus construction.

 

 

Example: Calculate the binding energy for the Helium atom  (42He)

 1. Calculate the mass defect

 

 

4.0026 a.m.u. - 4.0331 a.m.u. = -0.0305 a.m.u.

 

 2. Calculate the nuclear binding energy from E = mc2 ( 1 a.m.u. = 1.6605 x 10-27 kg)

 

 

E = (-0.0305 a.m.u.* 1.6605 x 10-27 kg/ 1 a.m.u.) * (3.00 x 108 m/s)2      ll

   = -4.55 x 10-12 kg m2/s2

 

What is a kg m2/s2?   It is the same thing as a joule (unit for energy)

 

-4.55 x 10-12 J.  This doesn't seem like much energy (basically 4 trillioniths of a joule). 

  But remember this is for one atom.  But what about many atoms?

 

4.0026 grams of Helium contains approximately 6.022 x 1023 atoms (This is called Avogadros number: see mole)

 

So,  -4.55 x 10-12 J/atom  * 6.022 x 1023 atoms  =  -2.74 x 1012 J   (This is over 2 trillion joules for just 4 grams)

 

ex. 1000 ton meteorite releases 5 x 1013 J. (1 kiloton TNT = 4.2 x 1012 J)

 

C. Types of Radioactive particles

- All radioactive decay reactions can be thought of an unstable parent nuclide decaying into a daughter nuclide.

 

1. Alpha Particles. High speed "helium nuclei". written as  42He or 42a.

Associated with heavy isotope decay (N > 83 and A >= 200)

ex.  21284Po ----> 20882Pb  +  42a  

 

Polonium was the first radioactive element found.  Discovered by Marie Curie and her husband Pierre in 1898.

20882Pb is the most abundant isotope of lead (~52.4%)

 

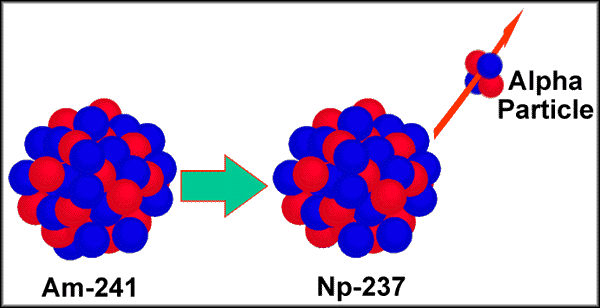
The alpha decay of 241Am (americium-241) to form 237Np (neptunium-237)

 

2. Beta Particles. High speed electrons. written as  0-1e- or b 

Associated with neutron decay.  10n ---> 11p  + 0-1e-

ex.   9843Tc  ---> 9844Ru  +  0-1b-

Technetium  is a radioactive element that does not occur naturally but instead was artificially prepared in 1937

 

 

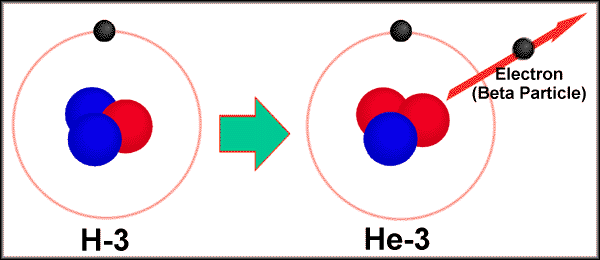
 Tritium (31H) decaying into 32He

What is Tritium? Click here to read about it.

Rutherford's discovery of the alpha and beta particles

Exercises in writing alpha and beta decay equations.

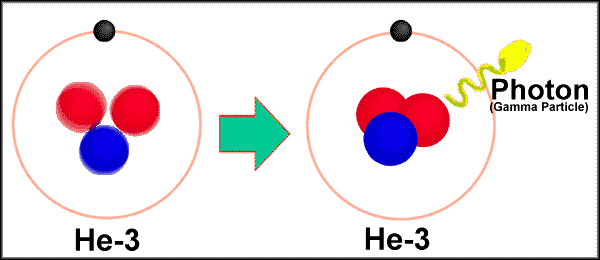
3. Gamma radiation.  Electromagnetic radiation with high frequency and high energy. written as g

Usually accompanies all radioactive emissions.  Represent lost energy. 

An interesting gamma emission.  The annihilation of an electron and a positron forms gamma radiation

0-1e-  +   0+1e ----> 2g   ( 0.511 MeV or 8.187 x 10-14 J)   ( 1 Megaelectron volt = 1.602189 x 10-13 J)

 

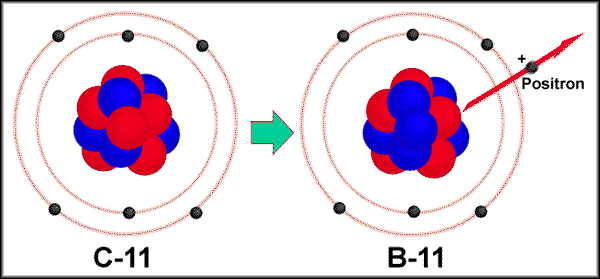
4. Positron emission-  Particle that is similar to an electron but with a positive charge.  written as 0+1e or b+

Positron emission essentially converts a proton into a neutron.  11p ---->  10n  +  0+1e

ex. Carbon-11 decay.      116C --->  115B +  0+1e.  

 

 

Positron annihilation studies at the University of Bristol, UK.

 

5. Electron capture- The nucleus captures an n=1 electron.  

Electron capture produces an effect similar to positron emission, converting a proton to a neutron.11p +  0-1e- ---->  10n  

ex. 74Be  +  0-1e-  --->  73Li.  

 

Exercises in writing positron emission and electron capture equations

 

 

 

D. Patterns of Stability

1. Neutron-to-Proton ratios

Nucleons are held together by Strong Nuclear Forces.  

The stability of the nucleus is dependent upon the neutron-to-proton ratio. As Z increases the number of neutrons needed also increases but not in a linear relationship.

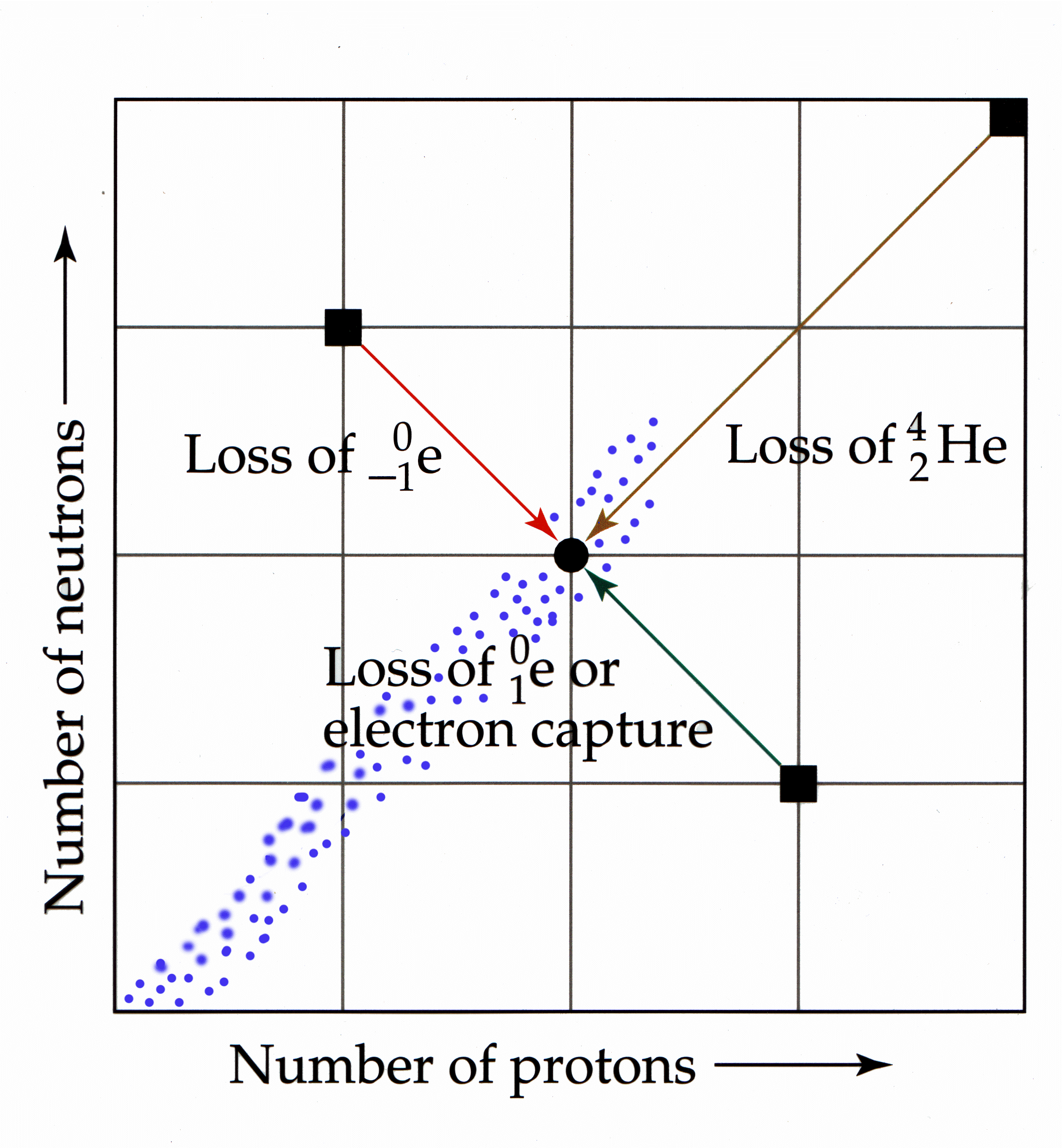
a. Belt of Stability.  A region on a neutron to proton graph that represents stable nuclides

Notes to Consider:

1. All nuclides with Z>83 are unstable

2. Z values lower than 20 have neutron/proton = 1

3. As Z increases above 20, the neutron/proton ratio increases.  ex. 90Zr = 1.25, 120Sn = 1.4, 200Hg = 1.5

4. Region above the belt represents excess neutrons

5. Region below the belt represents excess protons

 

 

 

 

Resource: Table of naturally found isotopes and abundances
 

Predicting decay based on neutron-to-proton ratio

Notes to consider:

1. Red Arrow: Represents high neutron/proton.  Seen as Beta Emission. Increases Z and A remains same

2. Brown Arrow:  Represents Z>83.  Alpha particles emitted to reduce both A and Z.

3. Green Arrow:  Represents low neutron/proton.  Positron emission or electron capture. Decreases Z and A remains same

 

 

b. Transmutation reactions.

Creating unstable nuclei from stable nuclei through bombardment of neutrons or other nuclei

The first transmutation was performed by Ernest Rutherford in 1919. Bombarding 14N with alpha particles

 

147N  + 42a  ---> 178O  +  11p+

Both the oxygen and hydrogen are stable so there is no further decay.

For transmutation reactions, the bombarding particle and the product particle are written in parentheses between the symbols for the reactant and product nuclides.  ex.   147N (a,p)178O

 

c. Nuclear decay series.  Nuclides with Z much larger than 83 cannot decay to stable nuclides with one emission.  This usually requires multiples steps representing multiple decay emissions. U-238 decays through a series of alpha and beta emissions before becoming stable.

 

           

An applet that demonstrate the decay series of some transuranium elements

  A historical perspective of where the names for the transuranium elements were derived.

A historic film showing transuranium elements. Hosted by Glenn Seaborg

 

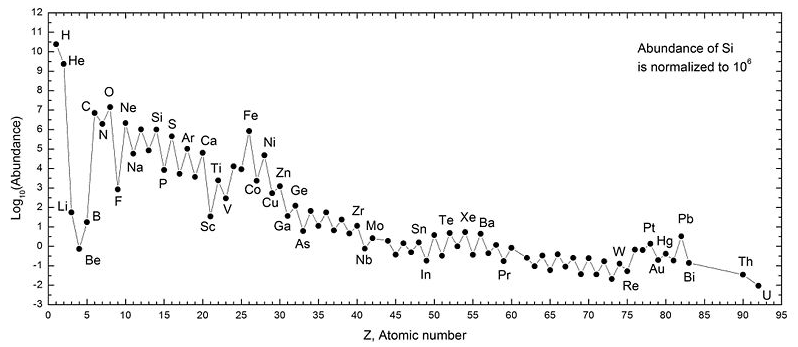
d. Stability based on nucleon numbers in an atom's nucleus.  Magic Numbers.  

Specific elements demonstrate a greater stability than others.  This is due to nucleon configurations.

1. Elements with Z = 2, 8, 20, 28, 50, and 82 are typically more stable than others

2. Elements with even-numbered Z and neutrons are generally more stable than odd-numbered nucleons

 

There are new elements being made that demonstrate a higher degree of stability than some.  Island of Stability

News release regarding the new elements Z = 116 and 118.

          Video on Island of Stability

 

E. Rates of Radioactive Decay

1. Half-Life:  The time to decay 1/2 of a sample of radioactive nuclides into their stable daughter nuclides

a. Decay rates are measured in disintegrations per time. Also known as a sample's activity

R  =  k N ; where R is activity (disintegrations per time), k is a decay constant, and N is the number of nuclides.

  k = 0.693/ t1/2  where t1/2  is the half life.  0.693 is the ln(2).  

*** We will discuss the origin of rate law expression later in Kinetics.

Applet: Identifying the rate of decay.

b. Calculating quantities of radionuclides.

sad
N   = number of radionuclides remaining after specific time (T)
N0 = number of original radionuclides
t    = Time
t1/2 = half life
Law of Radioactive Decay.  Relates the amount of decayed radionuclide to undecayed radionuclide

Practice: Looking at decay rates
       

c. Radioactive Dating 

A comparison of radioactive nuclei to the stable daughter nuclei in an artifact can predict the age.

Comparing the ratio of radioactive to stable nuclei in the same and then in the environment, scientists can infer the age by determining the number of half-life disintegrations. 

What is Carbon-dating?

Radioactive Decay Calculator

 

Table:  Naturally occurring isotopes and half-lives --  Half-lives of common isotopes

Resource: Common uses for radioisotopes --  The regulation & use of radioisotopes

III. Nuclear Fission and Fusion

Video tutorial of Fission and Fusion and the applications.

 

A. Fission. The splitting of heavy nuclei that results in the release of energy.

 

            fgd

B. Fusion.  The union of nuclides forming larger nuclide and the release of energy

          dgh

Nuclear Fusion in the Sun

       

 

 

References:  The types of decay diagrams are adapted from Thinkquest