Unit II. Electrons in Atoms

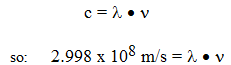I. Electromagnetic Radiation- energy that is emitted from the sun which has perpendicular electric and magnetic fields.

A. Electromagnetic Radiation spectrum- the compilation of electromagnetic waves emitted from the sun

1. All have a defined wavelength (l- lambda), the distance from one point of a wave to the similar point on the next

adjacent wave.

2. All have a defined frequency (n- nu), the number of wave cycles that occur in 1 second.

measured in hertz- (cycles/sec)

Simulation: Electromagnetic Waves. This shows the different types of waves based on wavelengths

Table: Wavelengths Frequencies & Energies of common electromagnetic waves.

Simulation: Electromagnetic & RADIO waves. Phet

3. The product of wavelength and frequency is a constant,

c = constant for speed of light = 2.998 x 10⁸ m/s, (186,282 mi/sec = 299,792,458 m/s)

Solving for wavelength & Frequency

Question: What is the relationship between wavelength and frequency? Click here to see.

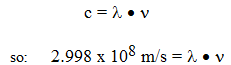** wavelength and frequency are inversely proportional**

Question: How was c determined? Michelson-Morley Experiment. Experimental evidence for the speed of light.

4. Visible light spectrum- 380 nm to 750 nm

B. Photons- a characteristic of the energy associated with electromagnetic radiation

1. Max Planck. (1858-1947). Developed the concept of the Quantum/Photon.

Quantum ("fixed amount")- the smallest, discrete packet of energy that is either released or absorbed by atoms.

a. Released energy is always an integer product of (h n)

b. A third characteristic of waves (frequency & wavelength) is amplitude, the intensity of a wave. This is measured as

the vertical height of a wave peak.

Calculating the Energy of a Photon

where h is Planck's constant (6.626 x 10^-34 Js). What is a Js?

in-class Practice: Calculating wavelength, frequency & energy.

on your own-practice: Electromagnetic Radiation Quiz:

C. Photoelectric Effect.

Albert Einstein developed the concept of electrons being liberated from atoms by absorbing photons.

(The link to Albert Einstein contains many pictures, quotes and some audio of his speeches)

Image: Photoelectric effect

Video: Photoelectric effect with different photons

II. Modern Theories of the Atom

A. Niels Bohr-(1885-1962)- 1913- Bohr Model of the Atom - Planetary Model

Resource: Discussion of Bohr Model

- Used Hydrogen to determine defined energy positions of electrons around the nucleus. (single electron)

- Stated that energy in electrons is quantized- discrete individualized values. Therefore electrons were restricted to certain

orbits about the nucleus, where orbits of greatest distance contain greater energy. Electrons in specified orbits do not emit any radiation

and therefore don't lose or gain energy.

- Energy is absorbed or emitted from electrons as they "jump" from one orbit to another. This is defined as a quantum of energy

- Quantum- the smallest amount of EMR that is absorbed or released by single electrons as they move between distinct orbits

- Energy level is another name for an orbit

Simulations: Bohr's Model -- Models of hydrogen atoms- PhET

Calculating the energy of an electron in the (n) energy level.

E = (-hcR_H)(Z² / n²)

Where R_H is the Rydberg constant, h is Planck's constant, c is the speed of light and Z is the atomic number, and n is the energy level

Ex. Find the energy of 1 electron in 1^st energy level of Hydrogen: [ (hcR_H)= 2.179 x 10^-18 J and Z = 1]

typically- Electron-volts are used calculating energies of electrons: 1 eV = 1.602 x 10^-19 Joules

Calculating the radius of an energy level

Radius of orbit = (n² a_o) / Z

Where n= energy level, a_o=radius when n=1 (0.529 A) and Z is the atomic number

Energies and Radii for subsequent energy levels:
N	Energy Level	Energy (eV)	Distance (A)
1	K	-13.595	0.529
2	L	-3.399	2.116
3	M	-1.511	4.761
4	N	-0.850	8.464
5	O	-0.544	13.225
infinity	--	0.000*	infinity
*The potential energy is set to zero at infinite distance from the nucleus, therefore bound electron states have negative potential energy

B. Atomic Spectra

Image: Line Spectra of Hydrogen Atom

1. States:

a. based on potential energies

1. Ground state- lowest energy an electron can have

2. Excited state- an electron at a higher energy level due to quantization

Video: Emission and absorption spectra

b. Series

1. Lyman- where n1 = 1 ultraviolet spectrum

2. Balmer- where n1 = 2 visible light spectrum. Balmer Formula

3. Paschen- where n1 = 3 infrared spectrum

Each series has a maximum frequency : additional absorbed energy would liberate the electrons from the atom

Robert Bunsen (namesake of the Bunsen Burner) is credited with being the father of modern spectroscopy

Bunsen & Kirchhoff's experiments on the reversibility of atomic emission specta

Emission Spectra is derived when electrons move from a higher energy level to a lower and release energy

Absorption Spectra is derived when electrons absorb specific wavelengths, moving electrons to higher energy levels,

while other wavelengths are allowed to pass through the atoms

Applet: Atomic emission and absoprtion spectrafor the elements.

c. Calculating the energy of spectral lines is dependent upon n_i and n_f, initial and final energy levels, respectively.

Simulation: Hydrogen atom simulator

in-class Practice: Calculating energy for spectral emissions

Calculations of Atomic Spectral Lines (Hydrogen specific)

E = (-hcR_H)(¹/n_f² - ¹/n_i²)

hcR_H= 2.18 x 10^-18 J, n_f = final energy level and n_i= initial energy level

Z = 1 for hydrogen. For any other element you must use Z²

Applet: Finding ground state & excited states (by orbitals) for spectral lines.

C. Quantum Model of the Atom - Video (What does an atom actually look like?)

- Based on the mathematical theory of Erwin Schrodinger- Austrian (1887-1961)

- Describes the relative position of electrons based on probabilities- orbitals- 3 dimensional

- The orbitals are less defined than Bohr's orbits, but still remain quantized.

- The shape of the orbital is described where a high probability of finding an electron exists. 90%

Example: 1^st orbital of Hydrogen- electron can exist up to 1 angstrom away from nucleus but has the highest probability at

0.529 angstroms. This describes a spherical cloud.

1. Electron density- high probabilities create a greater density whereas lower probabilities create a lower density.

Nodes are regions that separate electron dense areas.

2. Principles of the Quantum Theory- (Development of Quantum Numbers, Advanced discussion on Quantum Numbers)

a. The location of an electron cannot be determined exactly. Orbitals describe a volume where there exists a higher probability

of finding an electron

b. Orbitals can be defined by a Principal Quantum Number (n)- which describes the relative distance of the orbital from

the nucleus (integer values)

-Energy level or Shell- terms used to describe (n)

Energy Level Number	1	2	3	4	5	6	7
Symbol	K	L	M	N	O	P	Q

-Maximum number of electrons that can fit into an energy level is 2n².

c. Orbitals with the same (n) may have different shapes. Subshell Quantum Number (l)- Also called Subsidiary/Azimuthal

Quantum Number.

-include all integer values from l = 0 to l = n-1.

-The l value defines the number of nodal planes- a plane which has a probability of zero for finding an electron

Different shapes of subshells/ orbitals
l value (# of nodal planes)	orbital	shape
0	s-type	spherical
1	p-type	dumbbell
2	d-type	4-lobed / other
3	f-type	8-lobed / others
4	g-type	(???????)
5	h-type	(???????)

Comparative energies of the orbitals: s-types < p-type < d-type < f-types < .....

Image: Orbitals- s through d types

Resource: Grand Orbital Table showing shapes of orbitals up to n = 10

Possible orbitals for each Shell
Shell	n-value	Possible orbitals (l)	Types of orbitals
K	1	0	1s
L	2	0,1	2s, 2p
M	3	0,1,2	3s, 3p, 3d
N	4	0,1,2,3	4s, 4p, 4d, 4f
O	5	0,1,2,3,4	5s, 5p, 5d, 5f, 5g

d. For l values greater than zero. Orbitals with same l value have the same energy but different orientations- Magnetic Quantum

Number (m)- where m = -l to +l.

-degenerate orbitals- orbitals with the same l value- Subshell.

e. Electrons in orbitals will have Spin Quantum Number (s)- which defines either a clockwise or counterclockwise spin of

the electrons (s = + ¹/₂ or - ¹/₂)

- Parallel spins- electrons with same spin

- Only 2 electrons can exist in the same orbit- need to have opposite spins.

resource: Describing quantum numbers and practice

resource: Quantum Model of the atom. Electron's are more wave-like in motion than particle like.

Video: A better way to picture atoms

Image: Sodium atom with orbitals

resource: Quantum numbers & periodic table

in class practice: Quantum Number

on your own-practice: Quantum numbers & orbitals.

Question: How does this apply to atoms other than Hydrogen? Click here to begin the tutorial

3. Electron Configuration - the arrangement of electrons in the orbitals of an atom.

a. Described by 3 different terms

1. Number describing the principle

2. Letter describing orbital type (subshell)

3. Superscript describing the number of electrons it the subshell.

Tutorial. Electron Configurations of the elements.

b. Rules governing where an electron can fill

1. Aufbau- (building up)- electrons enter the orbitals with the lowest possible energies.

2. Pauli's Exclusion Principle- (Wolfgang Pauli) No two electrons can have the same set of 4 quantum numbers.

For 2 electrons to share the same orbital they must have opposite spins.

3. Hund's Rule- When filling a set of degenerate orbitals, the number of unpaired electrons will be maximized and these

electrons will have parallel spins.

4. Exceptions to Electron Configurations- [Cr, Cu, Nb, Mo, Ru, Rh, Pd, Ag, Pt, Au]

- Half and full-filled d orbitals are preferred over full s-type and partially filled d-filled orbitals

- Caused by interplay between pairing energy and promotion energy. Usually between s & d, and s, d, & f types.

on your own-practice:: Electron configurations exceptions quiz. Print off the results and include your answers/work

D. Heisenberg's Uncertainity Principle

It is impossible to determine accurately both the velocity and position of a particle simultaneously.

Gives rise to calculating probabilities of location = orbitals