ERROR ANALYSIS IN BIOLOGY
 

Error analysis in biology is no different from that in other sciences. Biology however is not an "exact" science in that much of the data collected by biologists is qualitative. Furthermore, biological systems are very complex and difficult to control. Biological investigations, nevertheless, do often require measurements and biologists do need to be aware of the sources of error in their data.

Human error

Obviously data which is carefully recorded will be more reliable than data collected carelessly. Human error can occur when tools or instruments are used or read incorrectly. For example a temperature reading from a thermometer in a liquid should be taken after stirring the liquid and whilst the bulb of the thermometer is still in the liquid. Thermometers and other instruments should be read with the eye level with the liquid otherwise this results in parallax error.

Human errors can be systematic because the experimenter does not know how to use the apparatus properly or they can be random because the power of concentration of the experimenter is fading.

Systematic errors

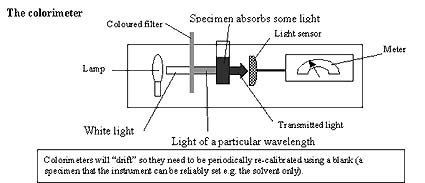
If an electronic water bath is set to 37°C the thermometer in the water bath should also read 37°C. If they do not agree then there will be an error at any other temperature being used. Some instruments need calibrating before you use them. If this is done correctly and regularly it can reduce the risk of systematic error.

Random errors

In biological investigations, the changes in the material used or the conditions in which they are carried out can cause a lot of errors.

For example the rate of respiration of a small animal measured using a manometric respirometer can be influenced by changes in air temperature and barometric pressure.

Biological material is notably variable.

For example, the water potential of potato tissue may be calculated by soaking pieces of tissue in a range of concentrations of sucrose solutions. However, different pieces of tissue will vary in their water potential especially if they have been taken from different potatoes.

The problem of random errors can be kept to a minimum by careful selection of material and careful control of variables (e.g. using a water bath or a blank).

As we saw above, human errors can become random when you have to make a lot of tedious measurements, your concentration span can vary. Automated measuring using a data-logger system can help reduce the likelihood of this error; alternatively you can take a break from measuring from time to time.

 

Replicates and samples

Because of their complexity and variability biological systems require replicate observations and multiple samples of material. As rule the lower limit is 5 measurements or a sample size of 5. Very small samples run from 5 to 20, small samples from 20 to 30 and big samples above 30.

Selecting data

Replicates permit you to see if data is consistent. If a reading is very different from the others it may be left out from the processing and analysis. However, you must always be ready to justify why you do this.

Degrees of precision

If you use a ruler, graduated in millimetres, to measure an object (e.g. the length of a leaf) you will probably find the edges of the object lie close to a millimetre division but probably not right on it. Recording the leaf is "4.5cm-and-a-bit" long is not very useful. The accepted rule is that the degree of precision is ± the smallest division on the instrument, in this case one millimetre. So the leaf in this example is 4.5cm ± 0.1cm.

The degree of precision will influence the instrument that you choose to make a measurement. For example of you used the same ruler to measure an object 0.5cm long the degree of precision (± 0.1cm) is 20% of the measurement, This a is very large error margin and, so, it is not very precise. Therefore, we must choose an appropriate instrument for measuring a particular length, volume, pH, light intensity etc.

The act of measuring

When a measurement is taken this can affect the environment of the experiment. For example when a cold thermometer is put in a test tube of warm water, the water will be cooled by the presence of the thermometer. When the behaviour of animals is being recorded the presence of the experimenter may influence them.

Why bother?

You might think that with all these sources of error and imprecision experimental results are worthless. This is not true, it is understood that experimental results are only estimates. What is expected of a scientist is that they:

  1. make the best effort to avoid errors in their design of investigations and the use of instruments.
  2. are aware of the source of errors and to appreciate their magnitude.

ELEMENTARY STATISTICS
Statistics are useful mathematical tools which are used to analyse data. Perhaps the best known statistic is the average. This is a single figure which is used to represent a set of data.

Averages

There are three types of average:

The median which is the middle value of a range of results.
The mode which is the value that appears the greatest number of times.
The mean which is the sum of all the results divided by the number of results.

Example: in the following set of data: 1; 3; 7; 10; 11; 12; 13; 13; 22; 23; 24

Note that if there are an even number of results the median is calculated by adding the middle two values and dividing by two.

Example: for the series 1; 2; 4; 5; 7; 9 the median = (4+5)/2 = 4.5

If all three averages are approximately the same we can usually assume that the data shows a "normal distribution" and the following tests can be used even for comparatively small samples (n<30).

Science usually works by taking samples rather than measuring every last item in a population.

The mean of the sample you have selected is not necessarily the mean of the whole population. Nor is it necessarily true that if the sample means taken from two different populations are different then the population means of each must be different. There is bound to be a natural variation. The tests on the next page determine how big the variation you obtain is in a sample.

Measuring the spread of the data

Averages do not tell us everything about a sample. Samples can be very uniform with the data all bunched around the mean or they can be spread out a long way from the mean. The statistic that measures this spread is called the standard deviation.

Arrange your data as follows and carry out the calculations:

 

Observations
e.g. Number of plants per quadrat

Frequency
e.g. Number of quadrats

    

x

f

xf

x2f

0

      

1

      

2

      

3

      

4

      

5

      

etc.

      
 

S f = n

S xf

S x2f

 

(Note: S = sum of ....)

The mean of the sample:
The standard deviation of the sample:

You can use a programmable calculator or a spread sheet to do this calculation for you after you have entered the data.

The standard deviation is a measure of the variation of the results. For data that is evenly distributed each side of the mean (a normal distribution) 68% of the data lies within one standard deviation of the mean.

Based upon material which may be found in Further Investigations in Biology (Vol. 1, 2, 3 and 4), Billiet, Casalis, Gaurenne & James, IBID Press.

 

THE MANN-WHITNEY U-TEST
Sometimes distributions of variables do not show a normal distribution, or the samples taken are so small that one cannot tell if they are part of a normal distribution or not. Using the t-test to tell if there is a significant difference between samples is not appropriate here.
The Mann-Whitney U-test can be used in these situations. This test can be used for very small samples (between 5 and 20). It can also be used when the variable being recorded is measured using an arbitrary scale which cannot be measured accurately (e.g. a colour scale measured by eye or a behavioural trait such as aggression).

The following example will illustrate the method.

The size of leaves taken from bramble bushes were measured to see if there is a difference between the size of the leaves growing in full sunlight and those growing in the shade.

 

Width of leaf / cm
Sunlight

6.0

4.8

5.1

5.5

4.1

5.3

4.5

5.1
Shade

6.5

5.5

6.3

7.2

6.8

5.5

5.9

5.5

The Mann-Whitney U-test is chosen because the sample size is so small it is not clear if these are samples taken from normally distributed data.

  1. Set up the Null Hypothesis: There is no difference between the leaves taken from the sunlit bramble and the shaded bramble.
    Alternative Hypothesis: There is a difference between the leaves taken from the sunlit bramble and the shade bramble.

     
  2. Let n1 be the size of the smallest sample and n2 be the size of the biggest sample.
    In this example both are of the same size so it does not matter which you choose.

    n1 = 8 and n2 = 8

     

  3. Rank all the values for both samples from the smallest (=1) to the largest. Set them up as shown in the table below.

Sunlight

Rank

Rank

Shade

4.1

1

    

4.5

2

    

4.8

3

    

5.1

4.5

    

5.1

4.5

    

5.3

6

    

5.5

8.5

    
   

8.5

5.5
   

8.5

5.5
   

8.5

5.5
   

11

5.9

6.0

12

    
   

13

6.3
   

14

6.5
   

15

6.8
   

16

7.2

R1 =

41.5

94.5

 = R2

Note where the values are the same and share the same rank, take an average of the rank values.
 

4. Total the ranks of each sample R1 and R2 (see the bottom of the table above).
 

5. Calculate the U values for both samples:

6; Use the table to find the critical value for the U statistic at the 5% level for samples of this size (n1 = 8 and n2 = 8).

Ucrit = 13
 

7. Reject the Null Hypothesis if the smallest value of U1 or U2 is below Ucrit. In this case U2 is below 13 we can reject the Null Hypothesis and accept the Alternative Hypothesis. The difference between the size of the bramble leaves in the light and the dark is significant for P>0.05. Bramble leaves in the dark seem to be significantly bigger.